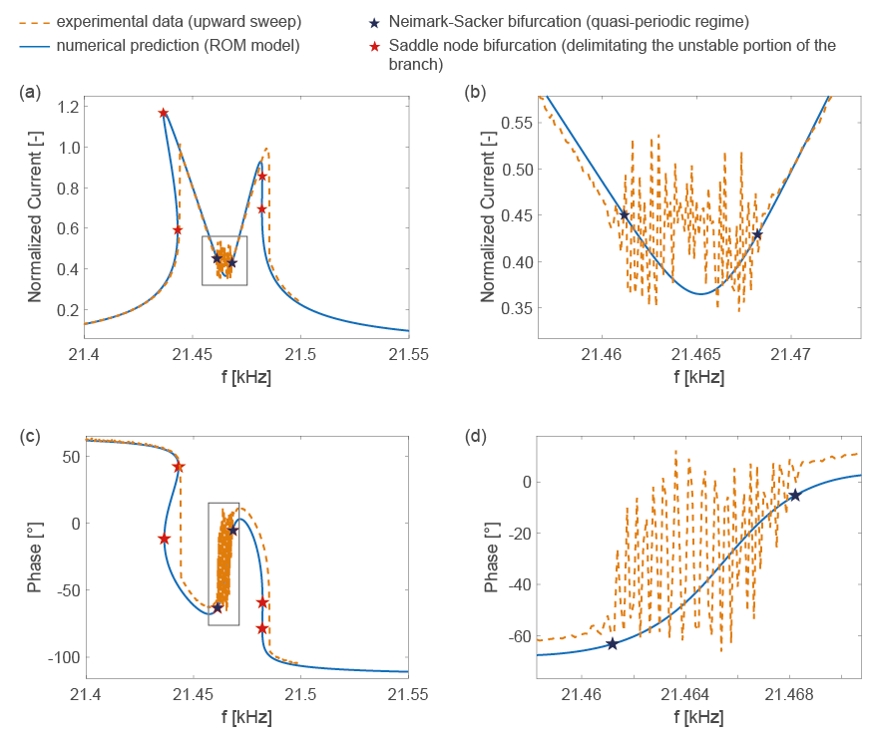
An example from [Gobat et al. 2021]
1:2 Internal Resonance in a MEMS gyroscope. Numerical simulation with a Reduced Order Model and validation with experimental data

.
Selected References
- A. Frangi, G. Gobat, Reduced Order Modelling of the non-linear stiffness in MEMS resonators, Int. J. Non-linear Mechanics, vol. 116, pp. 211-218, 2019
- A. Frangi, A. Opreni, N. Boni, P. Fedeli, R. Carminati, M. Merli, G. Mendicino, Nonlinear Response of PZT-actuated Resonant Micromirrors, IEEE JMEMS, 2020
- V. Zega , G. Gattere, S. Koppaka, A. Alter, G.D. Vukasin, A. Frangi, T.W. Kenny, Numerical Modelling of Non-Linearities in MEMS Resonators, JMEMS, vol. 29, n. 6, pp. 1443-1453, 2020
- Y Shen, N Béreux, A Frangi, C Touzé, Reduced order models for geometrically nonlinear structures: assessment of implicit condensation in comparison with invariant manifold approach, European Journal of Mechanics-A/Solids, 86, 104165, 2021
- Opreni, A.; Boni, N.; Carminati, R.; Frangi, A., Analysis of the Nonlinear Response of Piezo-Micromirrors with the Harmonic Balance Method, Actuators, vol. 10, n.21, 2021
- G Gobat, L Guillot, A Frangi, B Cochelin, C Touzé, Backbone curves, Neimark-Sacker boundaries and appearance of quasi-periodicity in nonlinear oscillators: application to 1: 2 internal resonance and frequency combs in MEMS, Meccanica, vol. 56, pp. 1937-1969, 2021
- A Opreni, A Vizzaccaro, A Frangi, C Touzé, Model Order Reduction based on Direct Normal Form: Application to Large Finite Element MEMS Structures Featuring Internal Resonance, Nonlinear Dynamics, vol 105, pp. 1237-1272, 2021
- G Gobat, V Zega, P Fedeli, L Guerinoni, C Touzé, A Frangi, Reduced order modelling and experimental validation of a MEMS gyroscope test-structure exhibiting 1: 2 internal resonance, Scientific Reports n. 11:16390, 2021
